










ENTREVISTA PARA A TV GAZETA

AFILIADA DA REDE GLOBO NO ESPÍRITO SANTO

ENTREVISTA PARA A FACULDADE DA
TV CANÇÃO NOVA - SP

ENTREVISTA PARA O JORNAL LOCAL
SAIBA NOTÍCIAS




REPORTAGEM NO JORNAL A TRIBUNA - 19/06/2022
TRIBUNA ERA AFILIDADA DO SBT NO ESPÍRITO SANTO




REPORTAGEM NO JORNAL A TRIBUNA - 11/09/2022
TRIBUNA ERA AFILIDADA DO SBT NO ESPÍRITO SANTO
SITE DO GOVERNO DO ESTADO DO ESPÍRITO SANTO - 31/05/2013
SITE DA SECRETARIA ESTADUAL DE EDUCAÇÃO - ES - 06/06/2013
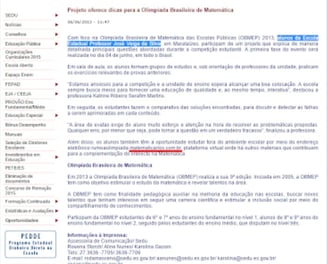
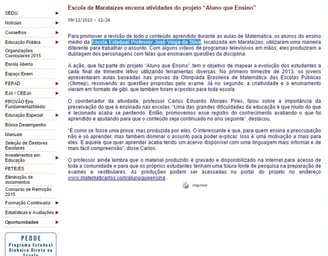
SITE DA SECRETARIA ESTADUAL DE EDUCAÇÃO - ES - 09/12/2013
DIÁRIO OFICIAL DO ESPÍRITO SANTO 25/04/2013


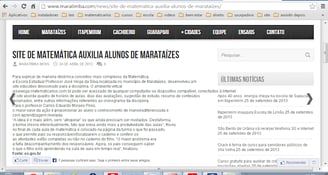
SITE LOCAL MARATIMBA - 24/04/2013
SITE DA SECRETARIA ESTADUAL DE EDUCAÇÃO - ES - 23/04/2013
ENTREVISTA PARA A TV GAZETA

AFILIADA DA REDE GLOBO - ES






















”Que vídeo gostoso de assistir, parecia que eu tava na na sala de aula! Gratidão prof”
@adynaguimaraes7846




”Estudei a 20 anos atrás hoje tenho que lembrar pra ensinar minha filha e nunca aprendi tão rápido assim. Nossa muito boa a explicação minha filha está pegado e estou conseguindo ensinar.”
@lucianafamilia3315
”Único professor que conseguiu tirar minhas dúvidas. Muito obrigado prof”
@PretinhoMoz


”Que vídeo gostoso de assistir, parecia que eu tava na na sala de aula! Gratidão prof”
@adynaguimaraes7846




”Estudei a 20 anos atrás hoje tenho que lembrar pra ensinar minha filha e nunca aprendi tão rápido assim. Nossa muito boa a explicação minha filha está pegado e estou conseguindo ensinar.”
@lucianafamilia3315
”Único professor que conseguiu tirar minhas dúvidas. Muito obrigado prof”
@PretinhoMoz

















